Multiple linear regression is a more practical version of simple linear regression. As a recap, simple linear regression uses the following equation:
However, simple linear regression is limited in it's efficacy because it can only make predictions based off of one feature. In the real world, there are often multiple features in data (e.g. for a house, some features would be its square footage, the number of stories it has, whether or not it has a pool, etc.). This gives us the motivation to use multiple linear regression, which can use multiple features to create predictions. The formula for the curve created by multiple linear regression is pretty similar to simple linear regression:
If you're thinking about the line on the 2D graph, Multiple Linear Regression is sort of a formulation of a multidimensional line. Given there are features, the multiple linear equation is:
Here, is the number of features there are, represents some particular feature, and represents the parameter that weights that particular feature. A higher value gives a higher weight to the feature it corresponds with, causing that feature to have a greater impact on the overall prediction.
Since there are multiple features, that means that the way we visualize multiple linear regression would have to be in multiple dimensions. For instance, with 2 features, we would have to represent data in 3-dimensions (two dimensions for each feature, and another dimension for the output). Here's what a multiple linear regression with 2 features could look like:
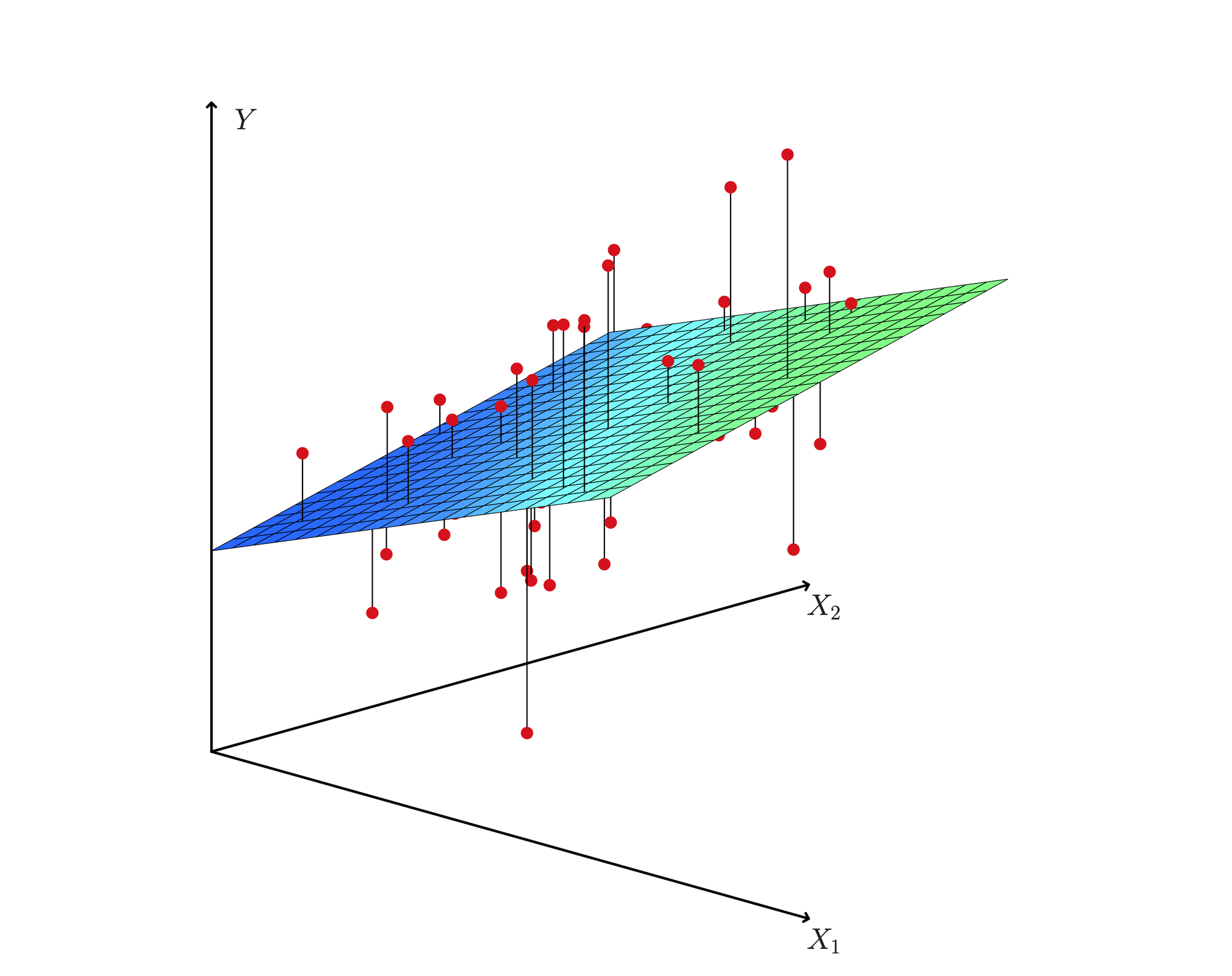
Notice how multiple linear regression generates a plane instead of a line in this instance. With even higher dimensional data, multiple linear regression would generate planes with even higher dimensions.
This is more applicable and can be used on real problems, because it can account for an infinite number of features — theoretically, of course. Real-world challenges tend to have features in the thousands or millions, and this is the first model equation you've learned that can handle that. Congratulations!
In the next lessons, we'll work on implementing multiple linear regression practically.
Next Section
Copyright © 2021 Code 4 Tomorrow. All rights reserved.
The code in this course is licensed under the MIT License.
If you would like to use content from any of our courses, you must obtain our explicit written permission and provide credit. Please contact classes@code4tomorrow.org for inquiries.